On considère la fonction $g$ définie par $g: x \mapsto \dfrac{1}{1-x^2}$
Démontrer que l'ensemble de définition de la fonction $g$ est $D_g =
]-\infty;-1[\cup ]-1;1[\cup]1;+\infty[ $.
En utilisant la calculatrice, construire le tableau de variations de la
fonction $g$.
Indiquer si les affirmations, en justifiant précisément, sont vraies ou
fausses :
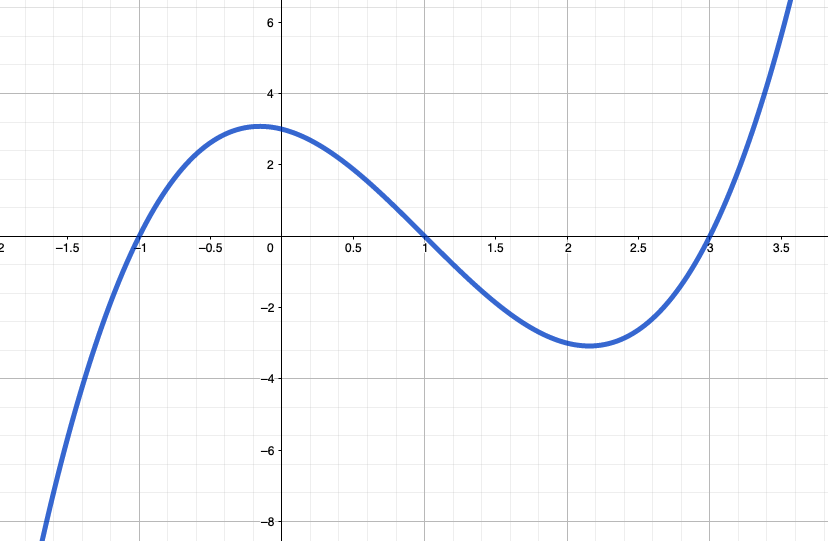
a. @hs5 Le maximum de la fonction $g$ sur $]-1;1[$
vaut $1$.
b. @hs5 $g(-8) < g(-7.9)$.
c. @hs5 $g(2) < g(2.1)$.
d. @hs5 L'équation $g(x) = 2$ possède deux
solutions.
e. @hs5 L'équation $g(x) = 1$ ne possède qu'une
seule solution.
f. @hs5 L'équation $g(x) = -4$ possède trois
solutions.
g. @hs5 L'équation $g(x) = 0.5$ possède deux
solutions.
h. @hs5 Pour $x \in ]-\infty;-2]$, $g(x) \leqslant
0$.
i. @hs5 Pour $x \in ]-1;1[$, $g(x) > 0.3$.
j. @hs5 Pour $x \in ]3;+\infty[$, $g(x) > 0$.
On considère deux antécédents $a$ et $b$ tel que $0
< a \leqslant b < 1$. Démontrer que $(a-b) \leqslant 0$ et $(a+b) > 0$
Démontrer que $(1-a^2) > 0$. Aide : factoriser
$(1-a^2)$ puis établir un tableau de signes (remarquer que $0 < a < 1$)
En s'inspirant de la question précédente, déterminer
le signe de $(1-b^2)$.
Démontrer que $g(a) - g(b) =
\dfrac{(a-b)(a+b)}{(1-a^2)(1-b^2)}$.
En déduire que $g$ est croissante sur $]0;1[$ et
vérifier le tableau de variations.
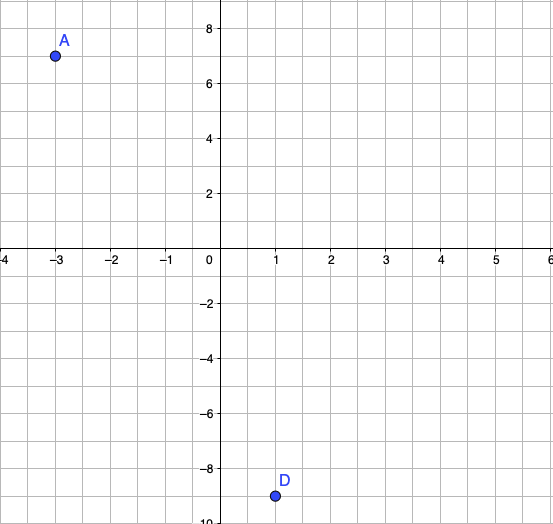 @vs5
Recopier et compléter le tableau et le graphique ci-dessus (placer les points manquants). Tracer la
représentation graphique $\mathcal{C}_n$ de la fonction $n$.
@vs5
Recopier et compléter le tableau et le graphique ci-dessus (placer les points manquants). Tracer la
représentation graphique $\mathcal{C}_n$ de la fonction $n$.