Médiane et quartiles
|
Le montant des dépenses (en euros) de chaque client lors d’une
journée de soldes a été relevé et trié dans le tableau ci-contre.
Déterminer la médiane, le premier et troisième quartiles. Déterminer aussi l'intervalle et l'écart inter-quartile. |
[
['Dépense en €','Nombre de clients' ],
['$[10;30[$','$46$' ],
['$[30;50[$','$74$' ],
['$[50;70[$','$28$' ],
['$[70;90[$','$62$' ],
['$[90;110[$','$31$' ],
['$[110;130]$','$19$' ],
]
|
|
Le tableau ci-contre indique la pointure d'un groupe d'élèves.
Déterminer la médiane, le premier et troisième quartiles. Déterminer aussi l'intervalle et l'écart inter-quartile. |
[
['Pointure' , 'Effectif' ],
['$35$' , '$78$' ],
['$36$' , '$82$' ],
['$37$' , '$43$' ],
['$38$' , '$21$' ],
['$39$' , '$17$' ],
['$40$' , '$5$' ],
]
|
|
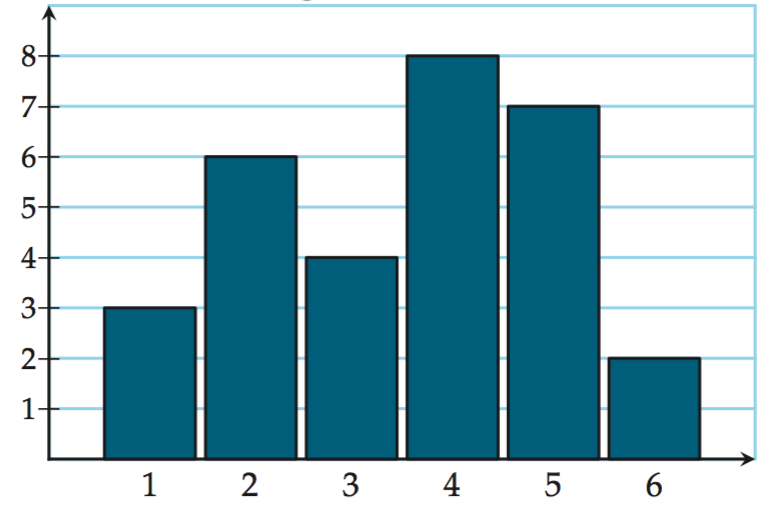
Une enquête réalisée auprès d’un groupe d’élèves pour
connaître le nombre d’enfants présents dans leur foyer est représentée par le graphique
ci-contre.
Déterminer la médiane, le premier et troisième quartiles. Déterminer aussi l'intervalle et l'écart inter-quartile. |
|
|
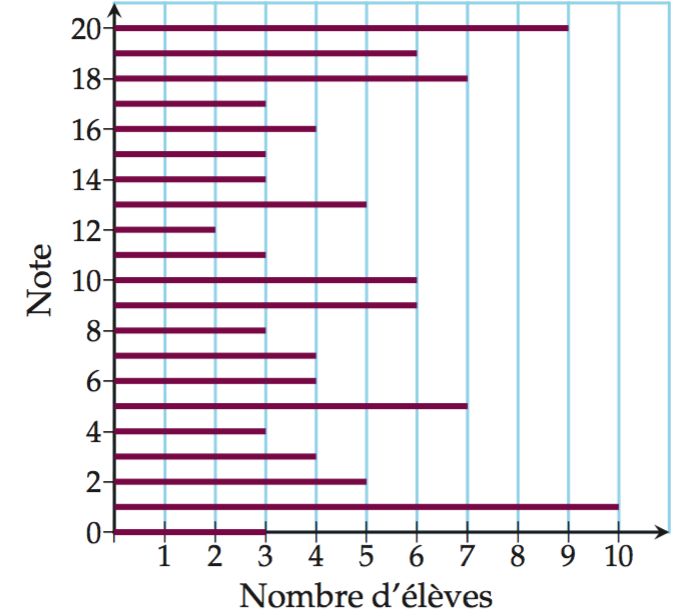
Voici les notes au dernier contrôle commun de trois classes de 2e
du Lycée de Mathyville.
Déterminer la médiane, le premier et troisième quartiles. Déterminer aussi l'intervalle et l'écart inter-quartile. |
|
|
Une entreprise vend des boîtes de $100\;g$ de maquereaux et
effectue des relevés de masse
Déterminer la médiane, le premier et troisième quartiles. Déterminer aussi l'intervalle et l'écart inter-quartile. |
[
['Masse en $g$' , 'Nombre de boîtes' ],
['$[95;97[$' , '$2$' ],
['$[97;99[$' , '$4$' ],
['$[99;101[$' , '$26$' ],
['$[101;103[$' , '$95$' ],
['$[103;105[$' , '$69$' ],
['$[105;107]$' , '$4$' ],
]
|