On considère la fonction $k$ définie par $k: x \mapsto 2x^2-4x-30$ de représentation graphique
$\mathcal{C}_k$.
@vs5 On considère, de plus, la fonction $g : x \mapsto -2x^2+8x+10$ de représentation graphique
$\mathcal{C}_g$.
Est-ce que la fonction $k$ possède un maximum ou un minimum ? Si oui donner sa valeur.
Justifier
par le calcul.
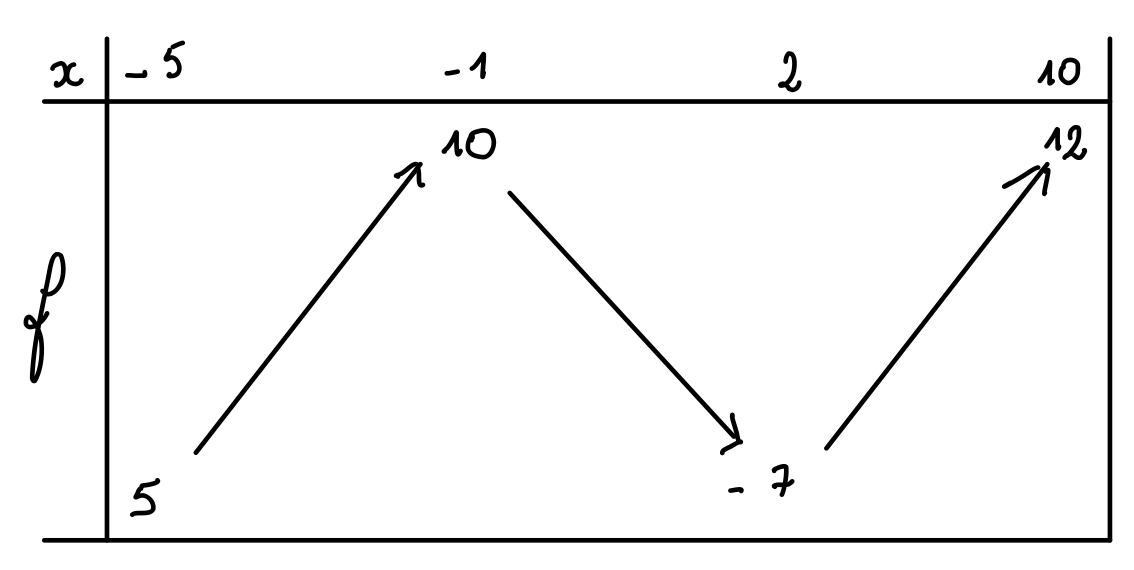
En déduire le tableau de variations de $k$. Justifier.
Est-ce que la fonction $g$ possède un maximum ou un minimum ? Si oui donner sa valeur.
Justifier
par le calcul.
En déduire le tableau de variations de $g$. Justifier.
Dans un même repère tracer très précisément $\mathcal{C}_k$ et $\mathcal{C}_g$. (il faut au
moins 7 points par courbe). Aucune justification n'est demandée. (On pourra prendre 1 cm pour 4 unités
sur l'axe
des ordonnées et placer l'origine du repère au centre de la feuille.)
Démontrer que $g(x) \geqslant k(x)$ $\ssi$ $-4x^2+12x+40 \geqslant 0$. On pose $f(x) =
-4x^2+12x+40$
Factoriser $f(x)$ puis résoudre $f(x) \geqslant 0$ en faisant un tableau de signes.
Retrouver, graphiquement, le résultat précédent. Expliquer en mettant des couleurs sur le
graphique.